Chapter

Quadratic equations are the equations of degree 2 i.e the highest power of the variable is 2. Therefore it has 2 solution or  2 roots.

The standard form of a quadratic equation is

Where a, b, c are constant numbers, x is the variable and  .  Before  deriving the general formula for a quadratic equation let us define the two terms.

Discriminant of the quadratic equation (D)

note that for real roots of a quadratic equation

Differential of a quadratic equation (D_f)

The differential of quadratic equation is given by .

Now the quadratic formula is derived as

or,

Note that RHS has two signs(+ and -), so it will give us the two roots which are the two solutions of the quadratic equation

Example 1

Here                                                               

Discriminant    

Differential D_f      

Putting in Quadratic formula

or

               or       

              or                

Hence    or  are the required solution or roots of the given equation.

Example 2

Here                  

Discernment 

Differential D_f     

Substitute in Quadratic formula

  or  

  or 

  or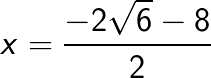  

i.e       or  are the required solutions

Example 3

Here                         

Discernment     

Differential   

Substituting in Quadratic formula

  or 

or

  or

So here both the solution are same (coincide) ,beacuse discriminant D = 0

Example 4

here                               

Discriminant   

Here as so on  real solution or roots are possible for this equation, so we need not proceed further.

Exercise                                                         Solution

                                    or

                                    or   

                                     or    

                                          or     

                                         or      

                                       or       

                                       or 

                                         or 

                                               or 

                                                or  

Corollary

Special types of quadratic equations which are of Reciprocal type can be solved by observation (Vilokanam) only.

Example 1

LHS is of reciprocal type so we have to break the RHS into two Reciprocal types

By comparing on both sides we can observe that  or     are the required solutions.

Example 2

So, X = 9  or X= 1/9

Example 3

Here or

or

or 

or 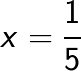     are

The two required solutions (note here that and are the reciprocal in LHS)

Exercise                                       Solution

                           X=5  or X=1/5

                            X=7 or X=1/7  

                              X=8 or X=-1/8 

                  X = -11/5 or x = -4/5 

                        or