Magic Stars
|
|||||||||
|
A 3 x 3 magic square with a solution |
This puzzle explores the world of magic stars, similar in concept to magic squares.
We explored magic squares in Magic Squares and More Magic Squares. In those puzzles we tried to arrange all the numbers from 1 to 9 in the boxes of a 3 x 3 square so that all rows, columns, and diagonals add up to the same number. Here is one solution to a puzzle in which the numbers in every row, column, and diagonal add up to 15.
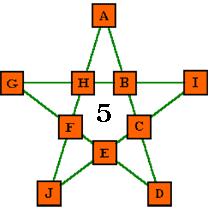
Magic stars take the magic squares concept and apply it to a star shape. Star 1 shows a magic star of order 5: a five-pointed star with a box at each vertex and intersection. There are 10 boxes altogether. Each has a letter in it. The problem: Is there any way to replace the letters A–H with numbers from 1 to 10 so that the sums of the number added along every line are the same. Each number may be used only once.
The “magic sum,” S, is found by adding all the numbers from 1 to 10. That sum is 55. When you add up all five lines in the star, you will get a sum that is 2 x 55, or 110 (because each number appears in exactly two different lines). Since the total of all the sums is 110 and there are five lines, the numbers along each line must sum to 110 / 5, or 22.
For each of the magic stars shown below, your challenge is to find a solution if one exists. One of the following magic stars has no solution. The others have many possible solutions. If there is no solution, can you show why? In each case you start by finding the magic sum, S, the amount that each line in the star must add up to. Solving these puzzles is a little bit like solving a sudoku puzzle. You start with one number and keep trying more numbers until you get to a contradiction. Then go back and try something else.
| 1. Magic star of order 5 (5 lines, numbers from 1 to 10) |
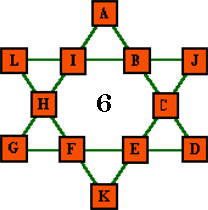
2. Magic star of order 6 (6 lines, numbers from 1 to 12) |
|
|
|
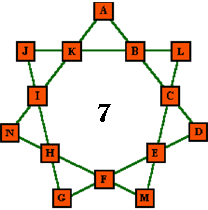
| 3. Magic star of order 7 (7 lines, numbers from 1 to 14) |
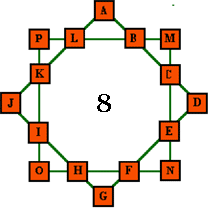
4. Magic star of order 8 (8 lines, numbers from 1 to 16) |
|
|
|
Background
Magic squares have been around and of interest to mathematicians for centuries. Magic stars represent a more modern form of combinatorics, and not as much is known about them. Magic stars come in many sizes and formats and tend to have many solutions. Mathematicians try to determine how many solutions exist for each type of magic star and how they are related. Some of this is discussed in master puzzler Martin Gardner’s book, Mathematical Carnival (Knopf, 1975). A number of Web sites are devoted to magic stars in all their many variations and intricacies. One of the best and most comprehensive is Magic Stars, created by Harvey Heinz. The graphics used for these problems were borrowed from Mr. Heinz with his permission from his Web site. If these problems intrigue you, check out the Web site.
This content has been re-published with permission from SEED. Copyright © 2026 Schlumberger Excellence in Education Development (SEED), Inc.