| |
Content |
Further guidance |
Links |
| 5.1 |
- Concepts of population, sample, random sample and frequency distribution of discrete and continuous data.
- Grouped data: mid-interval values, interval width, upper and lower interval boundaries.
- Mean, variance, standard deviation.
Not required:
- Estimation of mean and variance of a population from a sample.
|
- For examination purposes, in papers 1 and 2 data will be treated as the population.
- In examinations the following formulae should be used:

|
- TOK: The nature of mathematics. Why have mathematics and statistics sometimes been treated as separate subjects?
- TOK: The nature of knowing. Is there a difference between information and data?
- Aim 8: Does the use of statistics lead to an overemphasis on attributes that can easily be measured over those that cannot?
- Appl: Psychology SL/HL (descriptive statistics); Geography SL/HL (geographic skills); Biology SL/HL 1.1.2 (statistical analysis).
- Appl: Methods of collecting data in real life (census versus sampling).
- Appl: Misleading statistics in media reports.
|
| 5.2 |
- Concepts of trial, outcome, equally likely outcomes, sample space (U) and event.
- The probability of an event A as P( A)
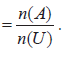 . .
- The complementary events A and A′ (not A).
- Use of Venn diagrams, tree diagrams, counting principles and tables of outcomes to solve problems.
|
. |
- Aim 8: Why has it been argued that theories based on the calculable probabilities found in casinos are pernicious when applied to everyday life (eg economics)?
- Int: The development of the mathematical theory of probability in 17th century France.
|
| 5.3 |
Combined events; the formula for P( A ∪ B) . Mutually exclusive events. |
. |
. |
| 5.4 |
- Conditional probability; the definition

- Independent events; the definition
- Use of Bayes’ theorem for a maximum of three events.
|
Use of P( A ∩ B) = P( A)P(B) to show independence. |
- Appl: Use of probability methods in medical studies to assess risk factors for certain diseases.
- TOK: Mathematics and knowledge claims. Is independence as defined in probabilistic terms the same as that found in normal experience?
|
| 5.5 |
- Concept of discrete and continuous random variables and their probability distributions.
- Definition and use of probability density functions.
- Expected value (mean), mode, median,variance and standard deviation.
- Applications.
|
- For a continuous random variable, a value at which the probability density function has a maximum value is called a mode.
- Examples include games of chance.
|
- TOK: Mathematics and the knower. To what extent can we trust samples of data?
- Appl: Expected gain to insurance companies.
|
| 5.6 |
- Binomial distribution, its mean and variance.
- Poisson distribution, its mean and variance.
Not required:
- Formal proof of means and variances.
|
- Link to binomial theorem in 1.3.
- Conditions under which random variables have these distributions.
|
- TOK: Mathematics and the real world. Is the binomial distribution ever a useful model for an actual real-world situation?
|
| 5.7 |
- Normal distribution.
- Properties of the normal distribution.
- Standardization of normal variables
. |
- Probabilities and values of the variable must be found using technology.
- The standardized value (z) gives the number of standard deviations from the mean.
- Link to 2.3.
|
- Appl: Chemistry SL/HL 6.2 (collision theory);Psychology HL (descriptive statistics); Biology SL/HL 1.1.3 (statistical analysis).
- Aim 8: Why might the misuse of the normal distribution lead to dangerous inferences and conclusions?
- TOK: Mathematics and knowledge claims. To what extent can we trust mathematical models such as the normal distribution? Int: De Moivre’s derivation of the normal distribution and Quetelet’s use of it to describe l’homme moyen.
|



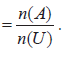 .
.